r.iresmi.net

R stuff so I can remember it

A photo of a dense crowd

Spatial autocorrelation

R
30DayMapChallenge
spatial
datavisualization

Day 29 of 30DayMapChallenge
2023-11-29
Michaël

A photo of three Adelie Penguin

Black & white

R
30DayMapChallenge
spatial
datavisualization

Days 24 & 25 of 30DayMapChallenge
2023-11-24
Michaël

A photo of Mount Fuji volcano

Tanaka

R
30DayMapChallenge
spatial
datavisualization

Day 23 of 30DayMapChallenge
2023-11-23
Michaël

A photo of arrows

North

R
30DayMapChallenge
spatial
datavisualization

Day 22 of 30DayMapChallenge
2023-11-22
Michaël

A photo of the Porcupine River in the Yukon Flats

Outdoors

R
30DayMapChallenge
spatial
datavisualization

Day 20 of 30DayMapChallenge
2023-11-20
Michaël

A photo of a clock

5-minute map

R
30DayMapChallenge
spatial
datavisualization

Day 19 of 30DayMapChallenge
2023-11-19
Michaël

A photo of a gannet in the sky

Birds in atmosphere

R
30DayMapChallenge
spatial
datavisualization
ecology

Day 18 of 30DayMapChallenge
2023-11-18
Michaël

A photo of a river flowing

Flow

R
30DayMapChallenge
spatial
datavisualization

Day 17 of 30DayMapChallenge
2023-11-18
Michaël

A photo of sea waves

El niño anomaly

R
30DayMapChallenge
spatial
datavisualization
remote sensing

Day 16 of 30DayMapChallenge
2023-11-16
Michaël

A photo of flowers in the shape of hearts

Defibrillator from OSM

R
30DayMapChallenge
spatial
datavisualization
OSM

Day 15 of 30DayMapChallenge
2023-11-15
Michaël

A photo of wind turbines on a beach in Bangui, Ilocos Norte, Philippines

Renewable energy in Europe

R
30DayMapChallenge
spatial
datavisualization

Day 14 of 30DayMapChallenge
2023-11-14
Michaël

A photo of Solutré-Pouilly, France

Choropleth

R
30DayMapChallenge
spatial
datavisualization

Day 13 of 30DayMapChallenge
2023-11-13
Michaël

A photo of Piedra de Culimacare on the Rio Casiquiare

Casiquiare

R
30DayMapChallenge
spatial
datavisualization
OSM

Day 12 of 30DayMapChallenge
2023-11-12
Michaël

A photo of a Roman road in Pompeii

Old map

R
30DayMapChallenge
spatial
datavisualization

Day 11 of 30DayMapChallenge
2023-11-11
Michaël

A photo of The Alte Nahebrücke, a medieval stone arch bridge in Bad Kreuznach, in western Germany, dating from around 1300

Bad map

R
30DayMapChallenge
spatial
datavisualization

Day 4 of 30DayMapChallenge
2023-11-04
Michaël

A photo of a female lynx posing on a dead tree

Clustering points to polygons

R
30DayMapChallenge
spatial
datavisualization

Day 3 of 30DayMapChallenge
2023-11-03
Michaël

A photo of tropical forest in Guadeloupe

OSM Guadeloupe trail relation

R
30DayMapChallenge
spatial
OSM
datavisualization

Day 2 of 30DayMapChallenge
2023-11-02
Michaël

A photo of lynx resting

Lynx from GBIF

R
30DayMapChallenge
spatial
datavisualization

Day 1 of 30DayMapChallenge
2023-11-01
Michaël

A map of the Aconcagua mountain consisting of isohypses

Mountains

R
spatial
datavisualization

Isohypses and T-shirts
2023-09-21
Michaël

A photo of a parquet

Fast remote parquet

R
Parquet
DuckDB

Magic!
2023-09-14
Michaël

Satellite image

Copernicus OpenEO NDVI time series

R
remote sensing

Use the OpenEO API to access Copernicus satellite datasets
2023-08-19
Michaël

A scatter plot with smoothed lines showing the number of controls by week and year

Where and when (not) to eat in France?

R
datavisualization
spatial

To eat or not to eat…
2023-04-16
Michaël

Cherry blossom

R
datavisualization

Plant physiology and climate
2023-04-05
Michaël

A puzzle

Open and merge multiple shapefiles, updated

R
spatial

One code to bind them all
2023-04-05
Michaël

A Mastodon post : Portugal 🇵🇹 borders only one country: Spain 🇪🇸

One neighbour

R
spatial

Contiguity analysis
2023-03-26
Michaël

A photo of a feral Cat Mom and 3 Kittens

Population growth

R
ecology

Cats, many cats
2023-02-10
Michaël

A view of Cilaos in Réunion Island

Map your Strava activities

R
datavisualization
spatial
sport

Use the Strava API to map your outings with R using the {rStrava} package.
2023-01-19
Michaël

Photo of Piton de la Fournaise and Formica Leo

Minimal

R
30DayMapChallenge
datavisualization
raster
spatial

Day 16 of 30DayMapChallenge
2022-11-16
Michaël

Photo of Rougaïl-saucisse dish

Food

R
30DayMapChallenge
datavisualization
spatial

Day 15 of 30DayMapChallenge
2022-11-15
Michaël

Photo of sugar cane fields

Sugar

R
30DayMapChallenge
datavisualization
spatial

Day 13 of 30DayMapChallenge
2022-11-13
Michaël

Photo of sale rulers

Scales

R
30DayMapChallenge
datavisualization
spatial

Day 12 of 30DayMapChallenge
2022-11-12
Michaël

Photo panorama of valley and mountains, Termignon, Vanoise National Park

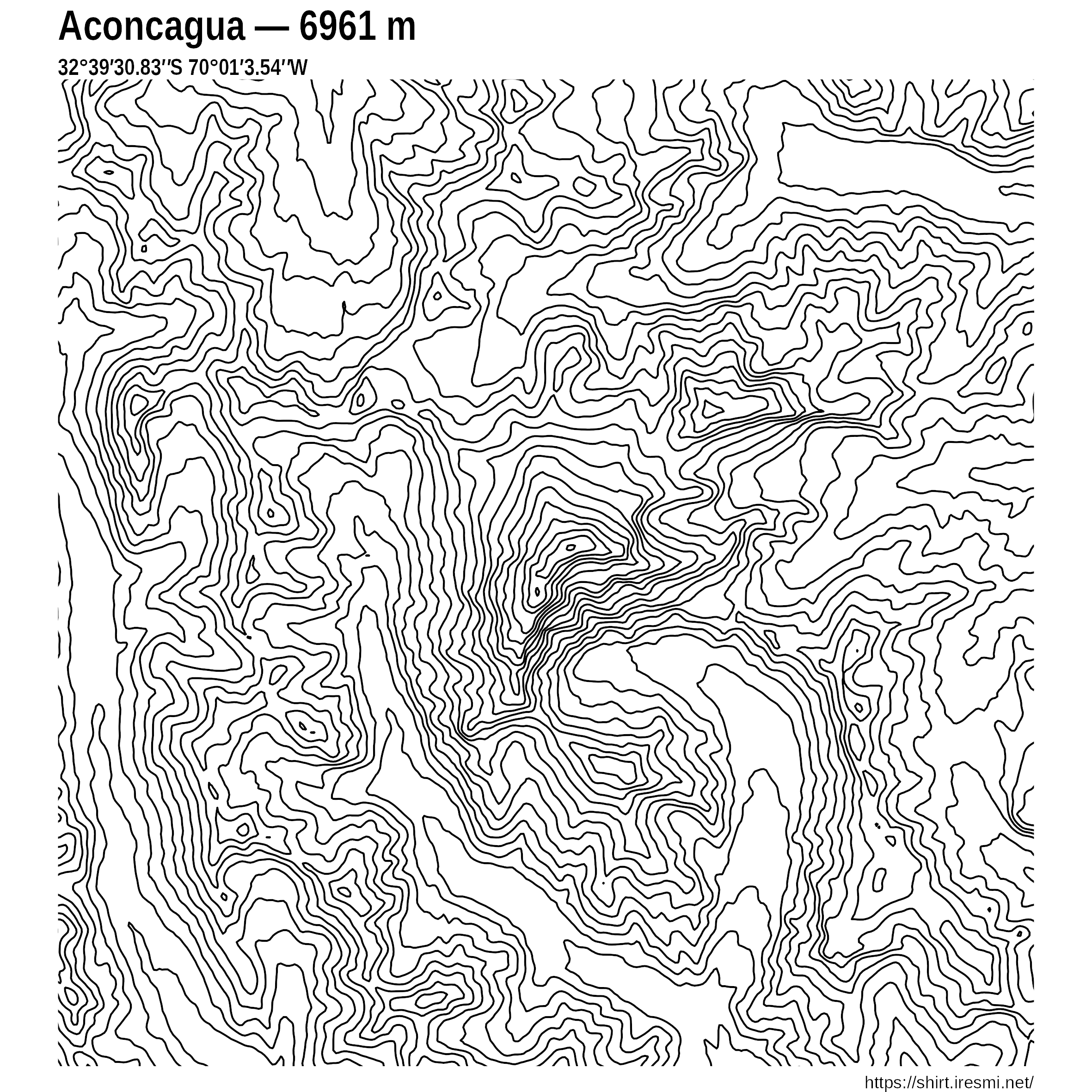
Sentinel

R
30DayMapChallenge
datavisualization
spatial
raster
remote sensing

Day 11 of 30DayMapChallenge
2022-11-11
Michaël

Get lost

R
30DayMapChallenge
datavisualization
spatial

Day 10 of 30DayMapChallenge
2022-11-10
Michaël

A photo of an Ariane 5 launch in Kourou

Use data from Wikipedia

R
30DayMapChallenge
datavisualization
spatial
webscraping

Day 9 of 30DayMapChallenge
2022-11-09
Michaël

A photo of a swimmer

The giant French Olympic-size swimming pool

R
30DayMapChallenge
datavisualization
spatial
OSM

Day 8 of 30DayMapChallenge
2022-11-08
Michaël

A photo of a high speed train

Use data from data.gouv.fr

R
30DayMapChallenge
datavisualization
spatial

Day 6 of 30DayMapChallenge
2022-11-06
Michaël

A photo of Kyiv, on the foreground: bridges on Dnieper

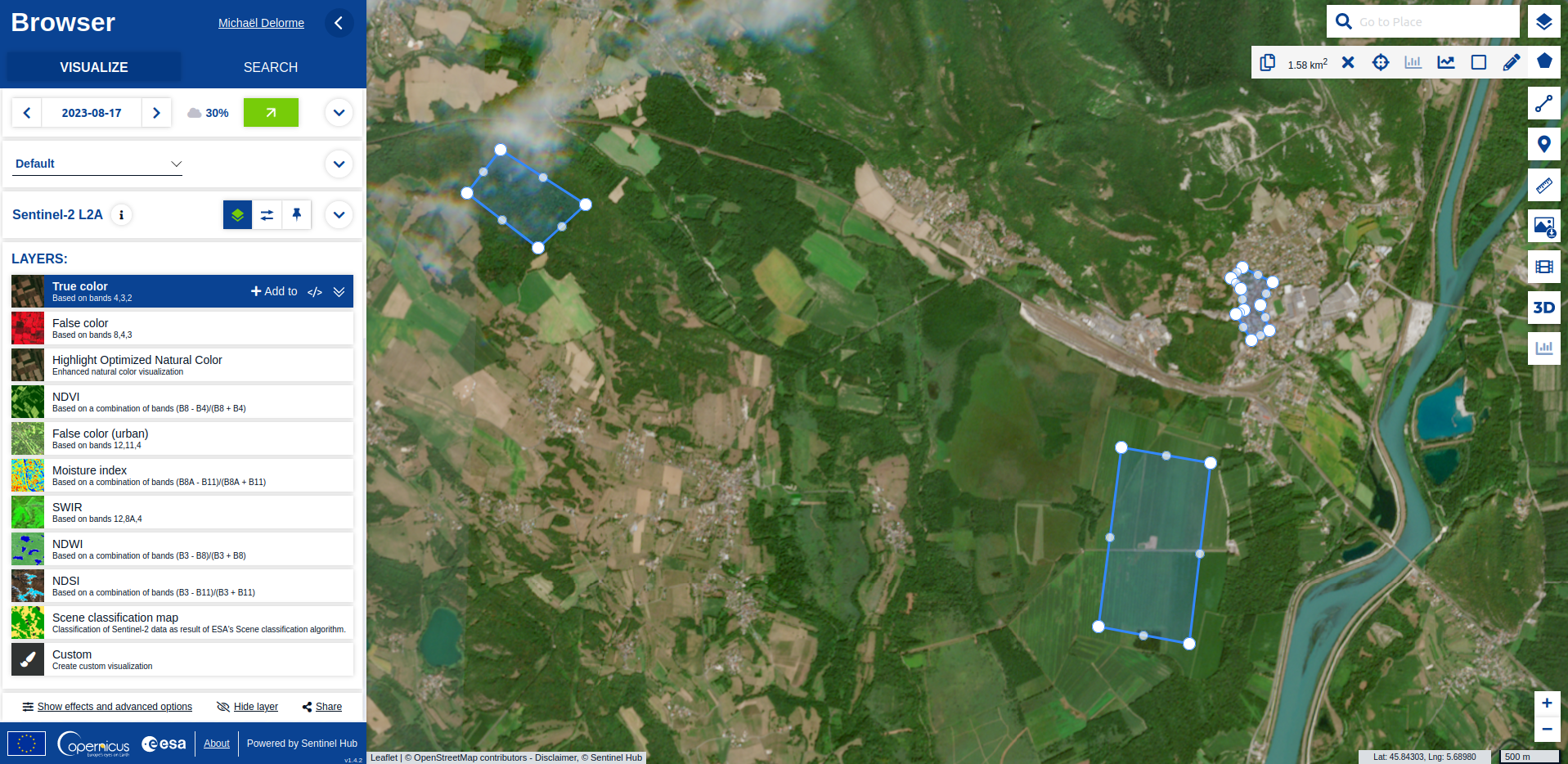
Use data from Openstreetmap

R
30DayMapChallenge
datavisualization
spatial
OSM

Day 5 of 30DayMapChallenge
2022-11-05
Michaël

A photo of A view just outside the village of Arsos, Limassol

Opening a spatial subset with {sf}

R
30DayMapChallenge
datavisualization
spatial

Day 3 and 4 of 30DayMapChallenge
2022-11-04
Michaël

Map of some airlines routes

My air travel carbon footprint

R
30DayMapChallenge
datavisualization
spatial

Day 2 of 30DayMapChallenge
2022-11-02
Michaël

A photo of of an old Suunto compass

Extract POIs from a Suunto watch

R
30DayMapChallenge
sport
spatial

Day 1 of 30DayMapChallenge
2022-11-02
Michaël

Simplifying polygons layers

R
french
spatial

Topology
2021-10-15
Michaël

A photo of a runner climbing on a trail during Transvulcania 2016

Does 100 m equal 1 km?

R
sport

Climbing or not climbing?
2021-09-16
Michaël

Playing with Roman numerals

R
What is the longest year number (yet) written in Roman numerals?
2020-12-25
Michaël

A photo of a trail runner

Trail running: is it worth starting?

R
modelling
webscraping
sport

Should I stay or should I go?
2020-08-10
Michaël

Using the geofacet package to spatially arrange plots

R
datavisualization
french
spatial
The {geofacet} package allows to “arrange a sequence of plots…
2020-06-15
Michaël

A photo of two alpine ibex

Generalized Monty Hall problem

R

Should I switch?
2020-06-12
Michaël

An animated map showing COVID death prevalence in 2020 in France

Polygons to hexagons

R
datavisualization
french
spatial

Hexagon tessellation using the great {geogrid} package
2020-05-26
Michaël

Animated map of COVID death prevalence in 2020 in Europe

Europe COVID-19 death map

R
datavisualization
raster
spatial
2020-05-02
Michaël

An animated map of smoothed COVID-19 prevalence in France in 2020

COVID-19 decease animation map

R
datavisualization
raster
spatial
french
2020-04-01
Michaël

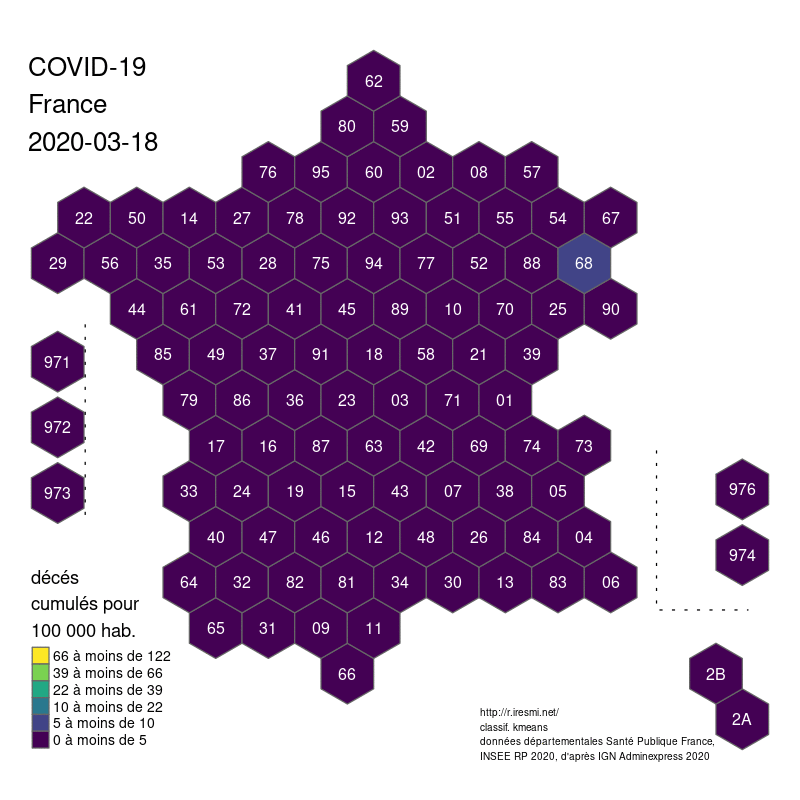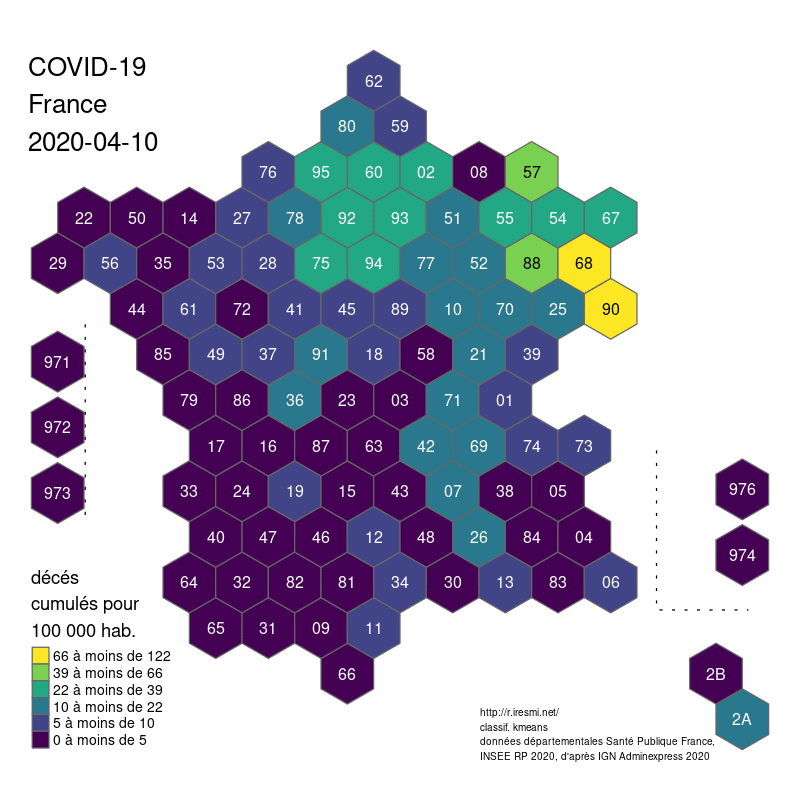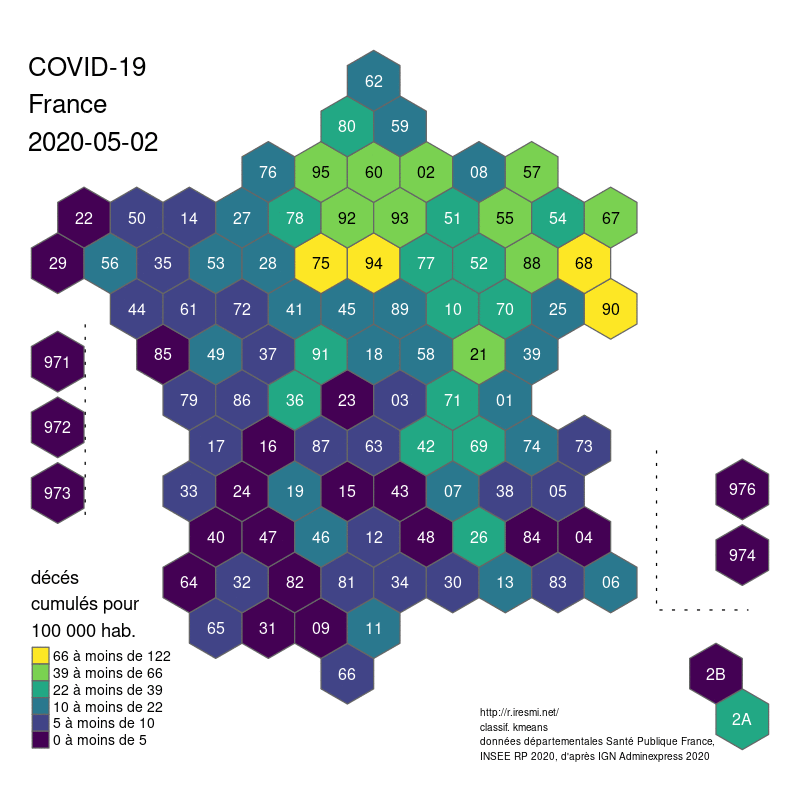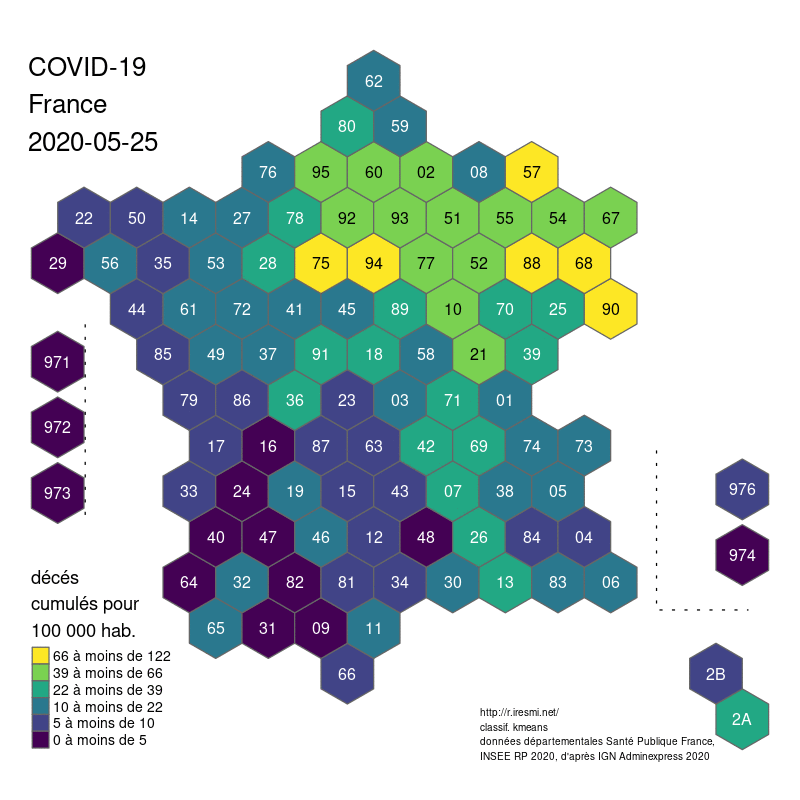
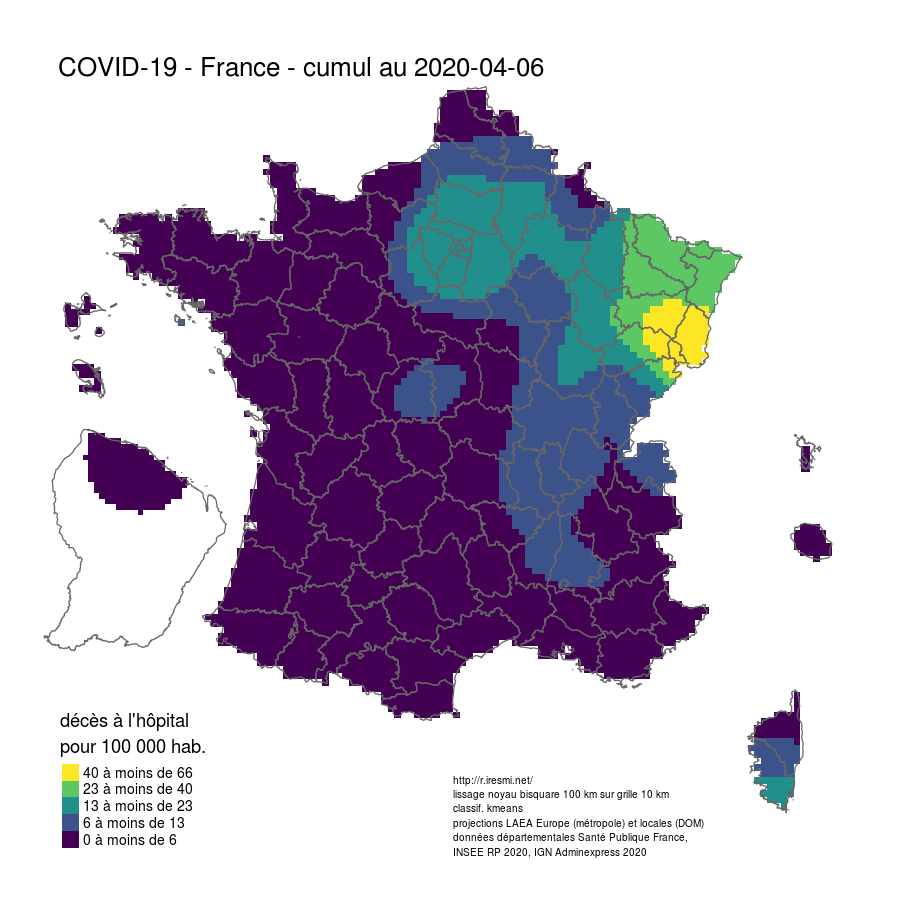
A map of smoothed death prevalence of COVID-19 in France, highlighting the strong prevalence in the NW

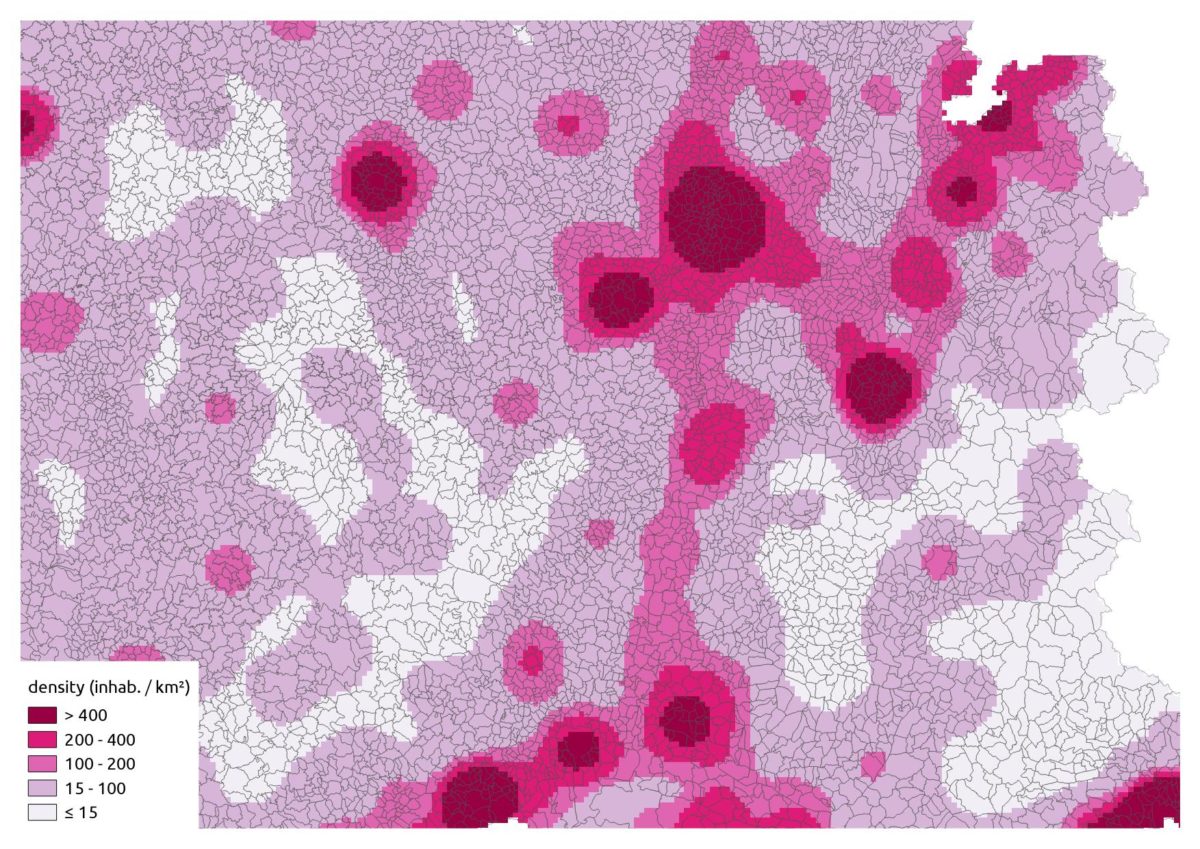
Coronavirus : spatially smoothed decease in France

R
french
raster
spatial
See also the animated map.
2020-03-30
Michaël

A plot of CO₂ atmospheric concentration in a spirale form

Mauna Loa CO₂ polar plot

R
datavisualization
i18n

Spiraling
2020-01-01
Michaël

Kernel spatial smoothing: transforming points pattern to continuous coverage

R
raster
spatial

Say no to choropleths (for mass data)
2019-05-11
Michaël

Metadata : from PostgreSQL comments to R labels

R
french
metadata
PostgreSQL
Metadata are an essential part of a robust…
2019-04-18
Michaël

Open and merge multiple shapefiles

R
spatial

or more precisely union many spatial tables in R in a tidy way
2019-03-27
Michaël

A scatter plot showing status number versus users by TLD instances

Post to Mastodon from R

R
Mastodon
Mastodon is a decentralized microblogging platform.
2019-02-15
Michaël

Aplot in norwegian showing the CO₂ atmospheric conentration rising from 315 to 410 ppm

Generate multiple language version plots

R
datavisualization
i18n
The use case is to create the same plot in different languages. I used this technique for Wikipedia plots.
2019-02-13
Michaël

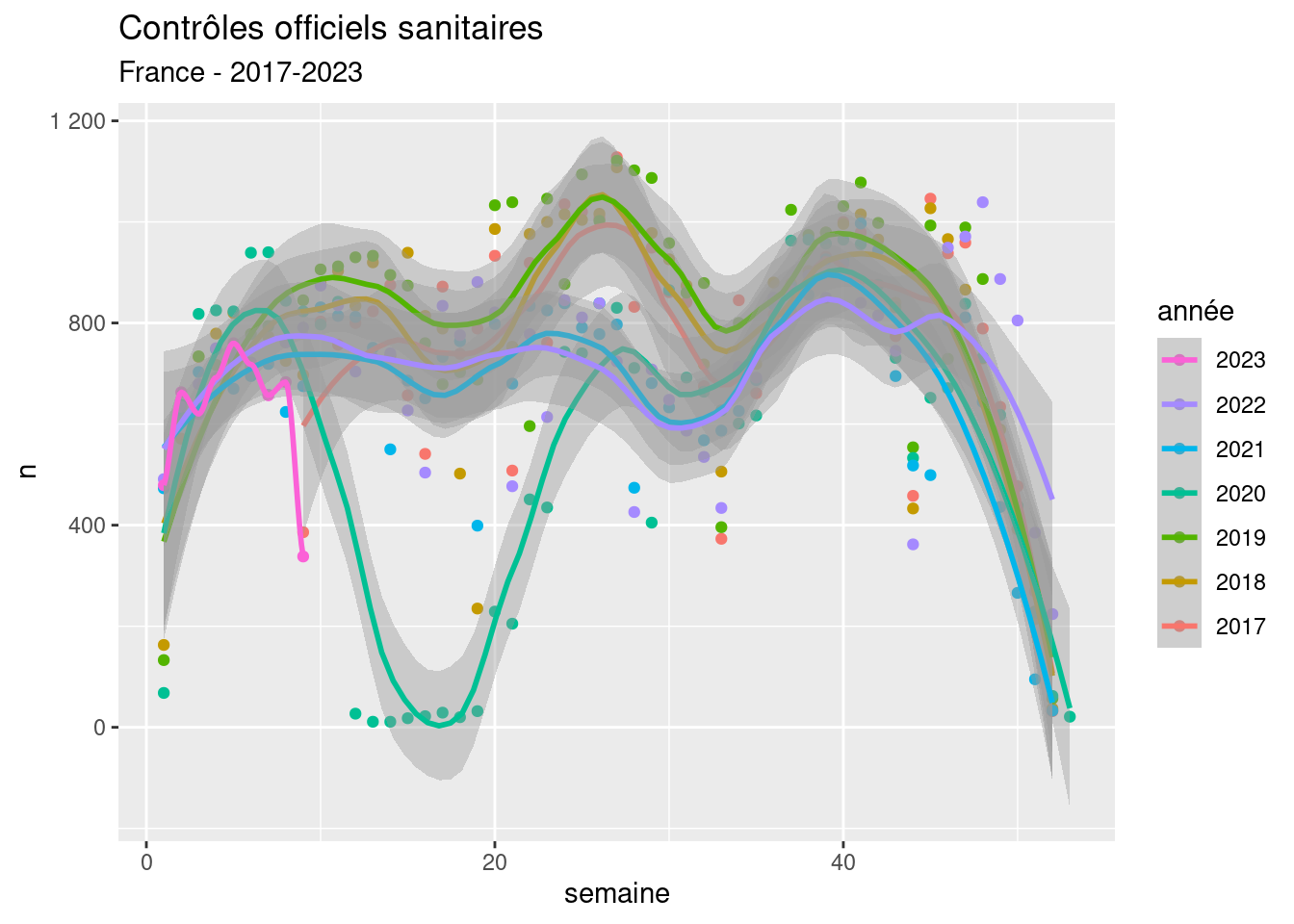
Mapping multiple trends with confidence

R
datavisualization
OSM
spatial
modelling

A tutorial to compute trends by groups and plot/map the results
2019-02-06
Michaël

Bibliography with knitr: cite your references and packages

R
Zotero

A tutorial to use your Zotero references with {rmarkdown} : easily add the citations, automatically generate your bibliography, including the references of the packages used in your analysis
2019-02-02
Michaël
No matching items